Federated Learning

, ,

I spent way too much time during my bachelor thesis diving into federated learning, and it turned out to be way cooler than I expected. The basic idea is pretty simple: what if we could train machine learning models without actually collecting everyone’s data in one place? Turns out you can, and there are some clever ways to make it secure too. Here’s what I learned while building my own implementation and writing my thesis.

What’s Federated Learning?

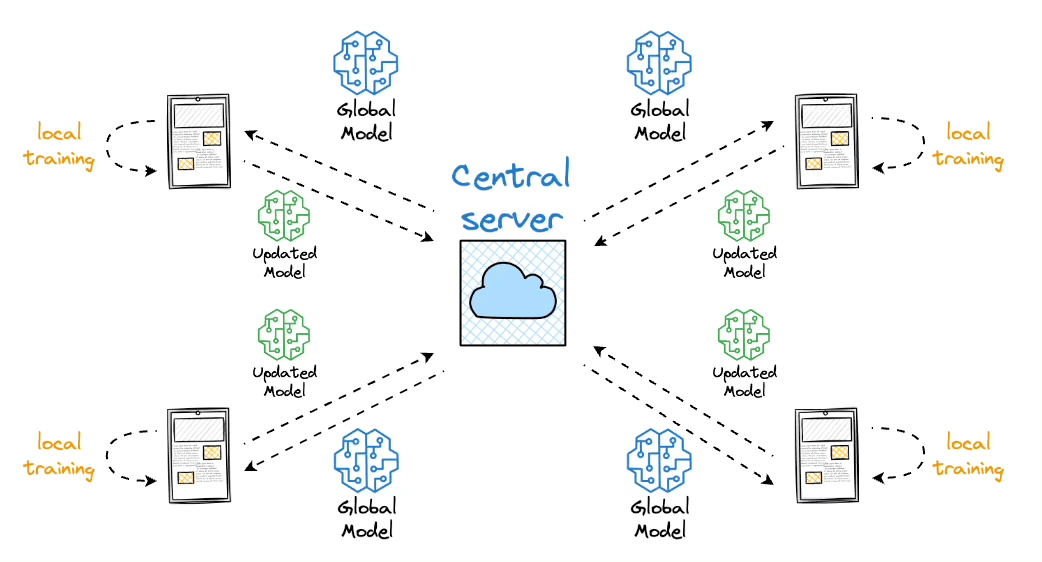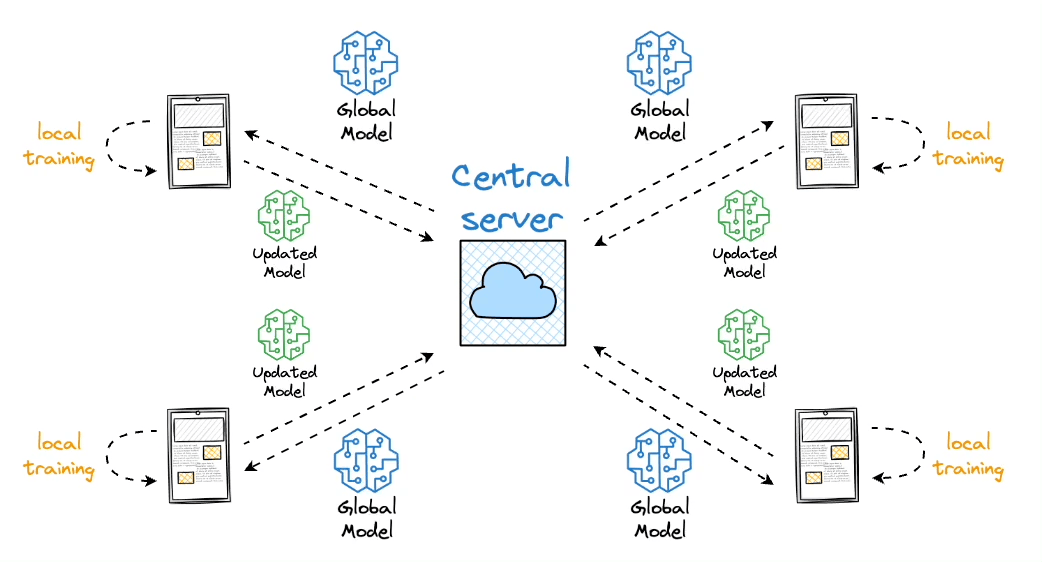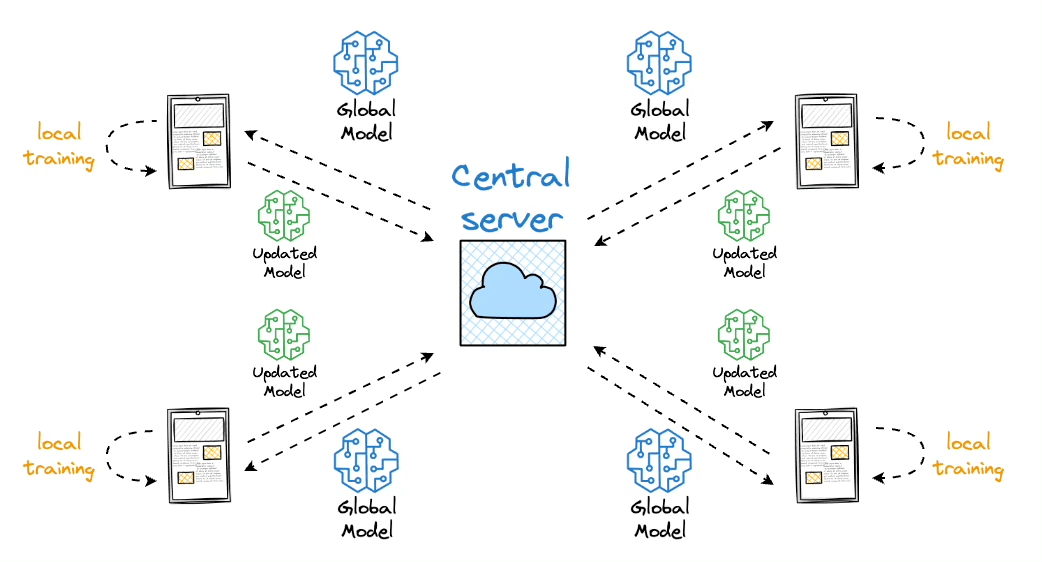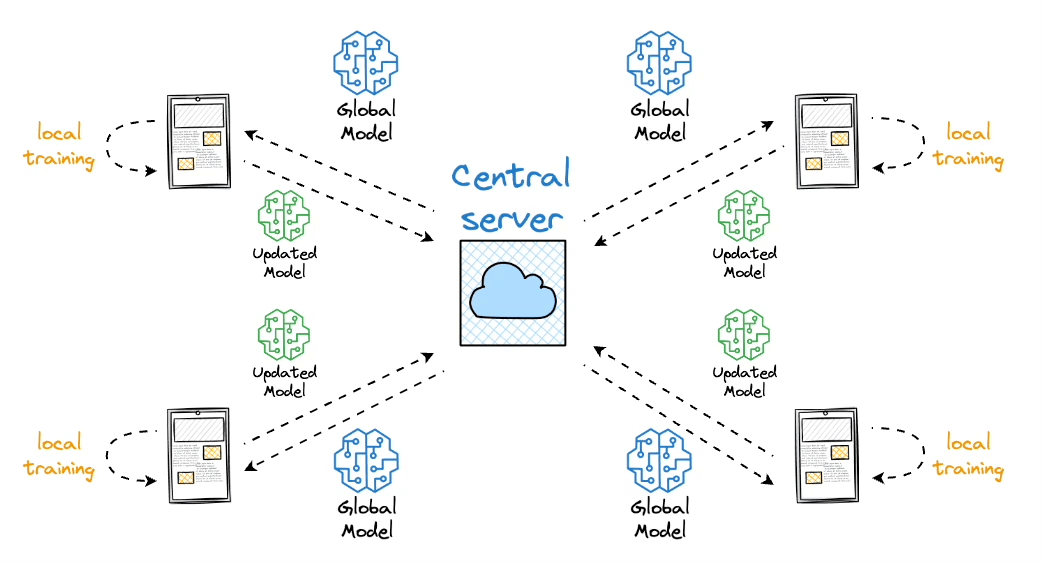
Usually when you train a model, you grab data from everywhere, dump it in one database, and train on that. Federated learning flips this around. Instead of moving data to the model, you move the model to where the data lives. Each device keeps its own data and just sends back what it learned.

The math looks like this: normally you’d minimize some loss function across all your data:

$$\min_{w\in\mathbb{R}^d} F(w) = \frac{1}{N}\sum_{i=1}^N \ell(x_i, y_i; w)$$

But with federated learning, you split this across different clients:

$$F(w) = \sum_{k=1}^K \frac{n_k}{n_{total}} F_k(w)$$

where each client $k$ has its own local loss $F_k$ with $n_k$ data points.

The process works like this:

  1. Send the current model to all clients
  2. Each client trains on their local data for a bit
  3. Clients send back their updates (not their data)
  4. Server combines all the updates into a new global model

Pretty neat way to keep data private while still getting the benefits of training on lots of data.

Basic Aggregation Methods

FedSGD

The simplest approach is FedSGD. Everyone does one gradient step and sends their gradient back:

$$w^{t+1} = w^t - \eta \sum_{k=1}^K \frac{n_k}{n_{total}} \nabla F_k(w^t)$$

This works but requires a lot of communication since you’re sending gradients after every single step.

FedAvg

FedAvg is way more practical. Let each client train for several rounds locally, then just average their models:

$$w^{t+1} = \sum_{k=1}^K \frac{n_k}{n_{total}} w_k^t$$

This cuts down communication dramatically and usually works just as well, though it can struggle when different clients have very different data.

Dealing with Bad Actors

One problem with federated learning is that some clients might send garbage updates, either by accident or on purpose. The simple averaging approach breaks down when you have outliers.

Geometric Median Aggregation

Instead of taking the arithmetic mean, you can use the geometric median, which is much more robust to outliers. You’re trying to find the point that minimizes the sum of distances to all client updates:

$$\min_z \sum_{k=1}^m \alpha_k ||w_k - z||$$

You solve this iteratively using something like the Weiszfeld algorithm:

$$z^{(i+1)} = \frac{\sum_{k=1}^m \beta_k^{(i)} w_k}{\sum_{k=1}^m \beta_k^{(i)}}, \text{ where } \beta_k^{(i)} = \frac{\alpha_k}{\max{\nu, ||w_k - z^{(i)}||}}$$

The math automatically gives less weight to updates that are far from the center, which helps filter out malicious or buggy clients.

Adding Differential Privacy

Even if clients only send gradients, a sneaky server might still be able to figure out things about the training data by analyzing those gradients carefully. Differential privacy fixes this by adding carefully calibrated noise.

The Core Idea

Differential privacy says that if you change one person’s data in the dataset, the output shouldn’t change much. Formally, a mechanism is $(\epsilon,\delta)$ differentially private if:

$$\Pr(\mathcal{M}(D) \in S) \leq e^\epsilon \Pr(\mathcal{M}(D’) \in S) + \delta$$

for any two datasets $D$ and $D’$ that differ by one record.

Making Federated Learning Private

In DP FedAvg, each client does two things before sending their gradient:

  1. Clip the gradient to a maximum norm:
    $$\tilde{g}_k = \frac{g_k}{\max(1, \frac{||g_k||_2}{C})}$$

  2. Add Gaussian noise:
    $$\hat{g}_k = \tilde{g}_k + \mathcal{N}(0, \sigma^2C^2\mathbf{I})$$

Here’s how you’d implement this:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np

def dp_clip_and_noise(
    grad: np.ndarray,
    clip_norm: float = 1.0,
    noise_multiplier: float = 1.0
) -> np.ndarray:
    """
    Clips and adds Gaussian noise to a gradient tensor for differential privacy.
    
    Args:
        grad: np.array representing the local gradient
        clip_norm: Max allowed L2 norm for the gradient
        noise_multiplier: Scales the noise relative to clip_norm
    
    Returns:
        np.ndarray: Anonymized gradient
    """
    # Clip
    norm = np.linalg.norm(grad)
    if norm > clip_norm:
        grad = (grad / norm) * clip_norm
    
    # Noise
    noise_std = noise_multiplier * clip_norm
    noise = np.random.normal(loc=0.0, scale=noise_std, size=grad.shape)
    
    return grad + noise

Now even if someone intercepts the gradients, they’re seeing a noisy version that doesn’t reveal much about individual data points.

Homomorphic Encryption

Differential privacy limits what you can infer from gradients, but homomorphic encryption goes further: the server never sees the actual gradients at all, only encrypted versions.

How It Works

Homomorphic encryption lets you do math on encrypted data. If you have encrypted values $Enc(a)$ and $Enc(b)$, you can compute:

$$Enc(a) \oplus Enc(b) = Enc(a + b)$$

without ever decrypting them.

For federated learning:

  1. Each client encrypts their update: $c_k = Enc(w_k)$
  2. Server adds the encrypted updates: $c_{sum} = \sum_{k=1}^K c_k$
  3. Someone with the private key decrypts the sum: $Dec(c_{sum}) = \sum_{k=1}^K w_k$

Here’s the basic idea in code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from typing import Any, Protocol

class HEContext(Protocol):
    """Protocol defining required methods for homomorphic encryption context"""
    def encrypt_zeros(self) -> Any: ...
    def homomorphic_add(self, a: Any, b: Any) -> Any: ...
    def decrypt(self, ciphertext: Any) -> Any: ...

def homomorphic_aggregate(
    encrypted_updates: list[Any], 
    he_context: HEContext
) -> Any:
    """
    Securely aggregates a list of encrypted updates using homomorphic addition.
    
    Args:
        encrypted_updates: List of encrypted model updates (ciphertexts)
        he_context: Context object providing homomorphic encryption operations
    
    Returns:
        Any: Single ciphertext representing the homomorphically summed updates
    """
    # Start with a ciphertext 'zero' in the correct scheme
    c_sum = he_context.encrypt_zeros()
    for c_u in encrypted_updates:
        # Homomorphic addition
        c_sum = he_context.homomorphic_add(c_sum, c_u)
    return c_sum

def decrypt_sum(c_sum: Any, he_context: HEContext) -> Any:
    """
    Decrypt the aggregated ciphertext to get the sum of plaintext updates.
    
    Args:
        c_sum: Encrypted sum of model updates
        he_context: Context object providing homomorphic encryption operations
        
    Returns:
        Any: Decrypted sum of the original plaintext updates
    """
    return he_context.decrypt(c_sum)

Putting It All Together

Here’s how a complete federated learning round might look with differential privacy:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np

def local_train(
    model_params: np.ndarray[np.float64], 
    local_data: tuple[np.ndarray[np.float64], np.ndarray[np.float64]], 
    epochs: int = 1, 
    lr: float = 0.01
) -> np.ndarray[np.float64]:
    """
    Train model parameters using gradient descent on local data.
    
    Args:
        model_params: Initial model parameters as numpy array
        local_data: Tuple of (X, y) arrays containing features and labels
        epochs: Number of training epochs
        lr: Learning rate for gradient descent
        
    Returns:
        np.ndarray: Updated model parameters as numpy array
    """
    w = np.copy(model_params)
    for _ in range(epochs):
        grad = compute_gradient(w, local_data)
        w = w - lr * grad
    return w

def compute_gradient(
    w: np.ndarray[np.float64], 
    data: tuple[np.ndarray[np.float64], np.ndarray[np.float64]]
) -> np.ndarray[np.float64]:
    """
    Compute gradient of MSE loss for linear regression.
    
    Args:
        w: Model parameters of shape (dim,)
        data: tuple of (X, y) where X has shape (num_samples, dim) 
             and y has shape (num_samples,)
             
    Returns:
        np.ndarray: Gradient vector of same shape as w
    """
    X, y = data
    preds = X @ w
    errs = preds - y
    grad = (X.T @ errs) / len(X)
    return grad

def federated_round(
    global_params: np.ndarray[np.float64],
    clients_data: list[tuple[np.ndarray[np.float64], np.ndarray[np.float64]]],
    clip_norm: float,
    noise_multiplier: float
) -> np.ndarray[np.float64]:
    """
    Execute one round of federated training with differential privacy.
    
    Args:
        global_params: Current global model parameters
        clients_data: list of (X, y) data tuples for each client
        clip_norm: L2 norm threshold for gradient clipping
        noise_multiplier: Scale of Gaussian noise for differential privacy
        
    Returns:
        np.ndarray: Updated global parameters after aggregating client updates
    """
    updated_params = []
    for local_data in clients_data:
        w_k = local_train(global_params, local_data)
        grad_k = w_k - global_params  # approximate local gradient
        grad_k_dp = dp_clip_and_noise(grad_k, clip_norm, noise_multiplier)
        updated_params.append(global_params + grad_k_dp)
    
    return np.mean(updated_params, axis=0)

# Example usage
if __name__ == "__main__":
    # Suppose we have a global 2D model parameter vector
    w_global = np.zeros(2)
    
    # Example: 3 clients with synthetic data
    clients_data = [
        (np.array([[1, 2], [0, 1]]), np.array([1.0, 0.0])),    # (X, y)
        (np.array([[3, 2], [4, 1]]), np.array([2.0, 3.0])),
        (np.array([[10, 2], [8, 2]]), np.array([4.0, 5.0]))
    ]
    
    # Run a few rounds
    for t in range(5):
        w_global = federated_round(w_global, clients_data, clip_norm=2.0, noise_multiplier=0.5)
        print(f"Round {t}, global params = {w_global}")

Real World Challenges

A few things I learned while implementing this stuff:

Non IID data is the biggest pain point. In the real world, different clients have totally different data distributions. Your phone’s photos look nothing like mine, which breaks a lot of the mathematical assumptions.

Client dropout happens constantly. Phones go offline, people close apps, connections fail. Your aggregation strategy needs to handle partial participation gracefully.

Privacy vs accuracy tradeoffs are real. Adding noise helps privacy but hurts model performance. Encrypting everything adds computational overhead. You’re constantly balancing security against practicality.

What I Learned

Building this federated learning system taught me that the theory is actually pretty straightforward, but the engineering challenges are where things get tricky. The math for differential privacy and homomorphic encryption looks intimidating, but the core ideas are simple once you get past the notation.

The most interesting part was seeing how all these techniques can work together. You can combine robust aggregation with differential privacy and homomorphic encryption to create systems that are resilient to both malicious attacks and curious servers.

If you want to dig deeper, check out my thesis and the code. The thesis goes into more detail about the performance tradeoffs and system design choices that matter in practice.