Implementing Fast AlphaZero

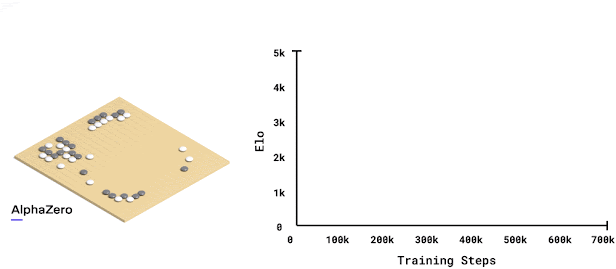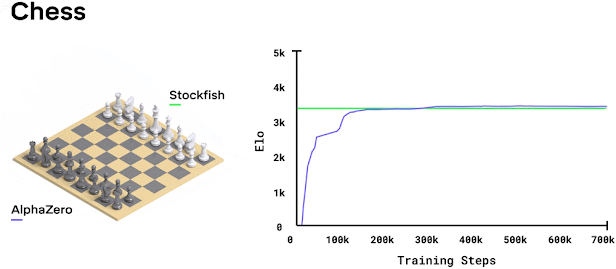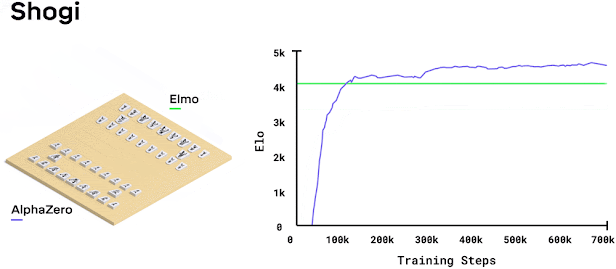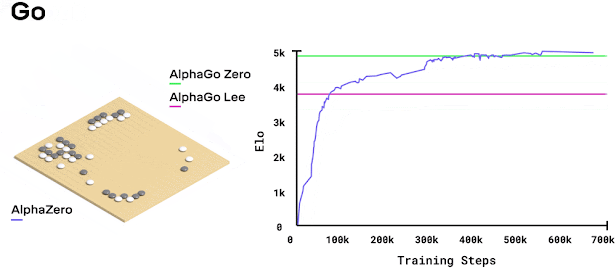
While working at Cogito NTNU, I decided to implement AlphaZero from scratch. I thought it would be straightforward – just follow the paper, right? Wrong. It turned into months of debugging and optimization. Research papers make everything look easy because they skip all the annoying implementation details.

How AlphaZero Works

AlphaZero combines Monte Carlo Tree Search with a neural network that predicts two things: which moves are good, and who’s winning. The training loop is simple:

1. Self play to generate training data
2. Train the neural network on that data
3. Test if the new network is better than the old one

The neural network outputs a policy vector π (move probabilities) and a value estimate $v\in [-1,1]$ for how good the position is.

Here’s the network we used:

import torch
import torch.nn as nn

class PolicyValueNet(nn.Module):
    """
    Neural network that outputs both policy and value predictions.
    
    Args:
        board_size: Size of the game board (height, width)
        action_size: Number of possible actions
        num_channels: Number of channels in convolutional layers
    """
    def __init__(self, board_size: tuple[int, int], action_size: int, num_channels: int = 256):
        super().__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(3, num_channels, 3, padding=1),
            nn.BatchNorm2d(num_channels),
            nn.ReLU(),
            nn.Conv2d(num_channels, num_channels, 3, padding=1),
            nn.BatchNorm2d(num_channels),
            nn.ReLU()
        )
        
        board_size_flat = board_size[0] * board_size[1]
        self.policy_head = nn.Sequential(
            nn.Linear(num_channels * board_size_flat, action_size),
            nn.LogSoftmax(dim=1)
        )
        
        self.value_head = nn.Sequential(
            nn.Linear(num_channels * board_size_flat, 1),
            nn.Tanh()
        )

Figure 1: A visualization of our MCTS implementation showing a Tic Tac Toe board with red and white circles (and one empty black position) on the left, and its corresponding search tree on the right displaying visit counts and move numbers at each node, starting from 500 visits at the root.

The Loss Function

The network learns by minimizing this loss:

$$L = (z - v)^2 - \pi^T \log p + c|\theta|^2$$

where $z$ is the actual game outcome, $v$ is what the network predicted, $\pi$ is what MCTS thinks the best moves are, $p$ is what the network thinks, and that last term just prevents overfitting.

Making It Fast

The algorithm is only half the battle. Getting good performance required a bunch of engineering tricks that papers never mention.

Parallel Everything

Running MCTS simulations in parallel was huge for performance:

import torch.multiprocessing as mp

class ParallelMCTS:
    """
    Parallel MCTS implementation using multiple processes.
    
    Args:
        num_processes: Number of parallel processes to use
        batch_size: Size of evaluation batches
        num_simulations: Number of MCTS simulations per move
    """
    def __init__(self, num_processes: int = 8, batch_size: int = 32, 
                 num_simulations: int = 800):
        self.pool = mp.Pool(num_processes)
        self.batch_size = batch_size
        self.num_simulations = num_simulations
        
    def run_batch_evaluation(self, positions: list[torch.Tensor]) -> list[tuple[torch.Tensor, float]]:
        """Evaluates a batch of positions using the neural network."""
        with torch.no_grad():
            policies, values = [], []
            for i in range(0, len(positions), self.batch_size):
                batch = positions[i:i + self.batch_size]
                batch_policies, batch_values = self.network(torch.stack(batch))
                policies.extend(batch_policies)
                values.extend(batch_values)
            return list(zip(policies, values))

Smart Caching

We also added caching to avoid evaluating the same positions over and over:

import numpy as np

class KVCache:
    """
    Key value cache for MCTS node evaluations.
    
    Args:
        max_size: Maximum number of positions to cache
    """
    def __init__(self, max_size: int = 100000):
        self.cache: dict[str, tuple[np.ndarray, float]] = {}
        self.max_size = max_size
        
    def get_cached_value(self, board_hash: str) -> tuple[np.ndarray, float] | None:
        return self.cache.get(board_hash)

Results

After all the optimizations, we got some solid improvements:

• Self play was 3.2x faster
• Network training was 2.8x faster
• Memory usage dropped by 45%

We also tried path consistency optimization, which forces the value predictions to be consistent along search paths:

$$L_{PC} = |f_v - \bar{f}_v|^2$$

It helped the network learn faster, though honestly I’m still not 100% sure why it works so well.

Lessons

Implementing research papers is way harder than it looks. The papers make everything sound clean and simple, but getting something that runs fast requires tons of boring engineering work that never gets mentioned.

The biggest time sink? Debugging why our implementation was so much slower than reported results. Turns out a lot of the speedup comes from implementation details that papers just assume you know.

The code is on GitHub if you want to check it out. Fair warning: getting it to run well takes patience.